
Arguments: An argument is a set of statements, one of which, the conclusion is taken to be supported by the remaining statements, the premises.
For example;
Premises: All men are mortal
Socrates is a man
Conclusion: Socrates is mortal
What is Argument?
In the above example, there are three statements, 1) All men are mortal, 2) Socrates is a man, and 3) Socrates is mortal. The premises of the Argument is the first two statement, and the last statement is a Conclusion. The statements of premises support the statement of conclusion. This type of arrangement is called an Argument.
UNIT VI – Logical Reasoning (Click below on the topic to read the study notes)
|
UGC NET Study Materials for Paper 1 (eBook with MCQ) ⇒ BUY NOW |
Forms of Arguments
There are three types of Arguments:
1. Deductive Arguments
2. Inductive arguments, and
3. Abductive arguments
1. Deductive Argument
An argument where the conclusion follows validly from the premises. In other words, an argument where the truth of the premises guarantees the truth of the conclusion.
Example:
Premises: All men are mortal
Socrates is a man
Conclusion Socrates is mortal
In the above example, the premises, all men are mortal, and Socrates is a man, give a guarantee the truth of the conclusion; Socrates is mortal. The conclusion follows the validity according to the premises.
2. Inductive Argument
An argument where the premises point several cases of some pattern and the conclusion states that this pattern will hold in general.
An inductive argument will not be deductively valid, because even if a pattern is found many times, that does not guarantee it will always be found. Therefore, an inductive argument provides weaker, less trustworthy support for the conclusion than a deductive argument does.
For Example:
Premises: We have seen 1000 swans, and
All of them have been white
Conclusion: All swans are white.
In the above example, we have seen just 1000 swans (not all in the world), and all of them have been white. But it does not mean that all swans in the world are white. White swans are a case of a pattern in those particular circumstances. Hence, we have concluded in general that all swans are white. But it might not be true actually. This type of arrangement of premises and conclusion is an example of an Inductive argument.
3. Abductive (or Hypothetico-Deductive) Argument
An argument that (i) points out a particular fact, (ii) points out that if a particular hypothesis were true, we would get this fact, and so (iii) concludes that the hypothesis is indeed true.
Abductive arguments seem to make an even bigger jump than inductive arguments. Inductive arguments generalize, while abductive arguments say that successful predictions “prove” theory is true. Abductive arguments are not deductively valid because false theories can make true predictions. So, true predictions do not guarantee that the theory is true.
Example:
Premises: These coins conduct electricity (fact)
If these coins are made of gold (hypothesis),
then they would conduct electricity (prediction).
Conclusion: These coins are made of gold.
Structure of Categorical propositions
A proposition is simply a claim about the world that has truth value. Every proposition can be expressed as a declarative (i.e., not a question or command) sentence.
Categorical Proposition is any statement which relates two classes or categories of entities. In other words, a categorical proposition is a proposition that relates two classes of objects. A class is a group of objects.
Example: Cats are mammals
Here, a class or category (Cats) are related to another class or category (Mammals). So, “Cats are mammals” is a Categorical proposition.
Components of Categorical Propositions
For a any categorical proposition, there are four components:
- Subject Term: First category or class
- Predicate Term: Second category or class
- Copula: The grammatical link (verb) between subject and predicate terms.
- Quantifiers: Words that specify the quantity of the subject and predicate terms.
Two Important terms of Categorical Proposition
Universal:
- Affirmative: ‘All’ (includes all of a class)
- Negative: ‘No’ (excludes all of a class)
Particular: ‘Some’ (includes part of a class)
Example: All cats are mammals
Here, All – Quantifier
Cats – Subject Term
Are – Copula
Mammals – Predicate term
Properties of Categorical Propositions
Each categorical proposition has both quantity and quality properties. The followings are the properties:
Quantity: The quantity of a categorical proposition is determined by the quantifier used.
Quality: The quality of a categorical proposition is determined according to whether the proposition asserts of denies an overlap between the classes.
Affirmative: if a proposition asserts an overlap between the classes or category named, the quality of the proposition is affirmative.
Negative: In this, a proposition denies an overlap between the categories or classes named,
Distribution: If the proposition refers to the entire class named by a term, that term is distributed and if it does not refer to the entire class named by a term, then the term is undistributed.
Types of Categorical Proposition
There are four types of categorical position:
- All politicians are liars (Universal Affirmative) – A
- No politicians are liars. (Universal Negative) – E
- Some politicians are liars. (Particular affirmative) – I
- Some politicians are not liars. ( Particular negative) – O
Universal Affirmative (A- Propositions): In a proposition, if every member of the subject class is also a member of the predicate class, then it is called Universal Affirmative Proposition. In other words, whole of one class is included or contained in another class.
In an example “All politicians are liars”, every member of the class of politicians, is a member of another class of liars.
An universal affirmative proposition can be written as: All S is P
S and P represent the subject and predicate terms, respectively. Such a proposition affirms that the relation of class inclusion holds between the two classes and says that the inclusion is complete, or universal.
Universal Negative (E- Proposition): The proposition in which no members of the subject class are members of the predicate class.
In an example “No politicians are liars”, no member of the class of politicians, is a member of another class of liars.
Systematically, Universal Negative proposition can be represented as: No S is P
Such a proposition affirms that the no relation of class inclusion holds between the two classes and says that the exclusion is complete, or universal.
Particular affirmative (I-proposition): The proposition in which at least one members of the subject class is also a member of the predicate class.
In an example “Some politicians are liars”, some member of the class of politicians, is a member of another class of liars.
Systematically, Particular affirmative proposition can be represented as: Some S is P
Particular negative ( O-proposition): The proposition in which at least one members of the subject class is not a member of the predicate class.
In an example “Some politicians are not liars”, some member of the class of politicians, is a member of another class of liars.
Systematically, Particular affirmative proposition can be represented as: Some S is not P.
A brief of Four Kind of Categorical Proposition
| Type | Quantifier | Subject | Copula | Predicate |
| A | All | S | are | P |
| E | All (No) | S | are not (are) | P |
| I | Some | S | are | P |
| O | Some | S | are not | P |
Classical Square of Opposition
The opposition is an immediate inference grounded on the relation between propositions which have the same terms, but differ in quantity or quality (or both).
For any formal opposition between two propositions, it is essential that their terms should be the same. There can be no opposition between two such propositions as these:
- All angels have
- No cows are
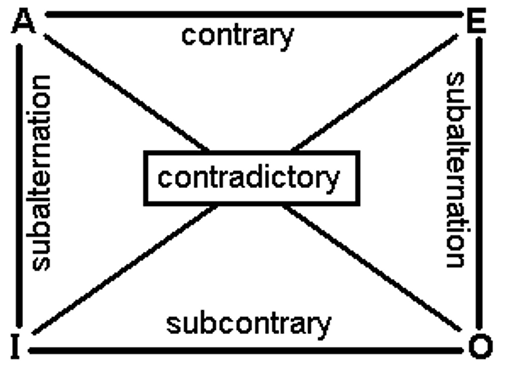
The square of opposition shows us the logical inferences (immediate inferences) we can make from one proposition type (A, I, E, and O) to another.

Contradictory: Two propositions are said to be contradictory if both cannot be true, and both cannot be false at the same time. In other words, if the opposition is between two propositions, which differ both in quantity and quality.
Here, A – All politicians are liars and O – Some politicians are not liars, and similarly, E and I propositions are contradictory.
Contrary: Universal propositions are said to be contrary because they cannot both be simultaneously true. In other words, the opposition is between two universals which differ in quality.A- All politicians are liars is true, the E- No politicians are liars must be false.
Similarly, if the E-proposition is true, then the A-proposition is false.
Sub-contrary: If the two particular propositions can both be true but cannot both be false. In other words, the opposition is between two particulars which differ in quality. It means that they cannot both be simultaneously false.Sub alternation: The universal to particular and particular to universal inferences are called subalternation. In other words, the opposition is between two propositions which differ only in quantity.
These inferences are valid if the subaltern (A or E) is true, then the subaltern (I or O) is true. If the subaltern is false, then the subaltern is false.
Categorical Syllogism
A syllogism is an argument containing two premises and a conclusion.
Categorical syllogism: A categorical syllogism is a syllogism whose premises and conclusion are categorical propositions.
For example:
Premises:
- All hats are fashionable clothing.
- All fashionable clothing is purple.
Conclusion:
- So, some hats are purple.
A Standard Form Categorical Syllogism Contains:
- Two premises and a conclusion, each a standard form categorical proposition.
- Major Term: A major term which appears only in the first premise and the predicate of the conclusion.
- Minor Term: A minor term which appears only in the second premise and the subject of the conclusion
- Middle Term: A middle term which appears in both premises but not in the conclusion.
- Major Premises: The major premise is the premise which contains the major term.
- Minor Premise: The minor premise is the premise which contains the minor term.
Mood and Figure of Syllogism
The categorical syllogisms can be categorise as:
- The kind of standard form categorical proposition which appears as its first (i.e., major) premise,
- The kind of standard form categorical proposition which appears as its second (i.e., minor) premise, and
- The kind of standard form categorical propositions which appears as its conclusion.
Mood:
When the major premise, the minor premise, and the conclusion of a categorical syllogism arranage in a series of three letters (A, E, I, or O) corresponding to the type of categorical proposition is called MOOD of an argument.
Example:
Premises: All P are M
All S are M
Conclusion: Some S are P
The first premise is of the form A
The second premise is of the form A
The conclusion is of the form I.
Thus, the mood of this Argument is AAI.
In another example, to figure out the FORM of the premises and the conclusion in the following example:
Premises: No S are P (E-propostion)
Some S are P (I-Proposition)
Conclusion: Some S are not P (O-Proposition)
Thus, the mood of this Argument is “EIO”.
When you have to determine the mood of a categorical syllogism, you need to find out which of the four forms of categorical proposition each line of the Argument is (A, E, I, or O).
Figure:
The figure of a categorical syllogism is a number which corresponds to the placement of the two middle terms.
For example, consider the following arguments:
P 1. All mammals are creatures that have hair.
P 2. All dogs are mammals.
P 3. Therefore, all dogs are creatures that have hair.
Notice that the middle term in the major premise is on the LEFT, while the middle term in the minor premise is on the RIGHT. Whenever this happens, we say that the argument has figure “1.”
There are four possible figures in the categorical syllogism:
Figure1: When the middle term is on the left in P 1, and on the right in P 2.
Figure2: When the middle term is on the right in both premises.
Figure3: When the middle term is on the left in both premises.
Figure4: When the middle term is on the right in P 1, and on the left in P 2.
Important Points of Mood and Figures:
- There are 64 different moods
- And each mood has 4 different figures.
- Thus, there are 64*4=256 different kinds of standard form categorical syllogisms.
Valid Argument Forms
There are two kinds of valid argument forms:
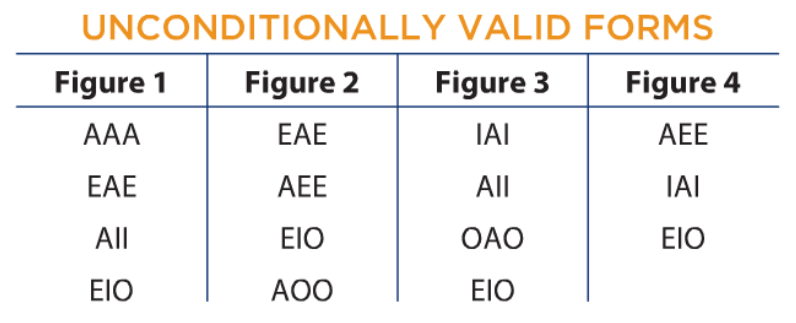
Unconditionally Valid Forms: There are fifteen combinations of mood and figures that are valid from the Boolean standpoint, and we call these “unconditionally valid”argument forms. The chart below depicts ALL of 15 the unconditionally valid argument forms.
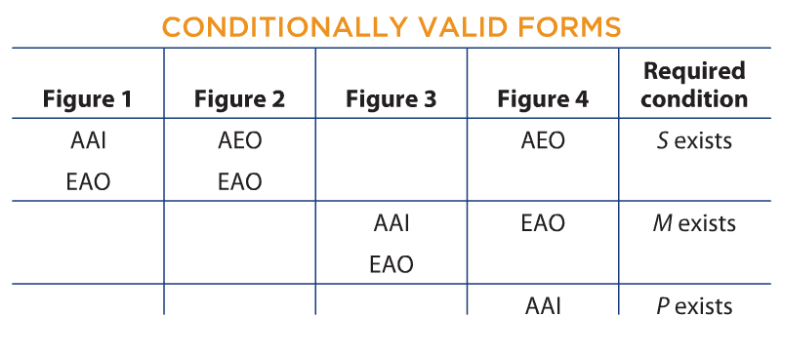
Conditionally Valid Forms: There are some inferences that are NOT valid from the Boolean standpoint, which is valid from the Aristotelian standpoint. In addition to the fifteen unconditionally valid argument forms, there are nine conditionally valid argument forms for categorical syllogisms:
Rules For Validity
A standard form categorical syllogism is valid on the modern theory if and only if each of the following five propositions is all true of it. A standard form categorical syllogism is valid on the traditional theory if and only if each of the first four propositions is true of it.
- The middle-term is distributed at least once.
- If a term is distributed in a conclusion, then that term is distributed in one of the premises.
- There is at least one affirmative premise.
- There is a negative premise if and only if there is a negative conclusion.
- If both premises are universal, then the conclusion is universal.
Informal and Formal Fallacy
Simply, a fallacy is a mistake in reasoning. In other words, a defect in an argument that misleads the mind is called a fallacy. There are two types of fallacy:
Formal Fallacies: A fallacy in which there is the involvement of an error in the form, arrangement, or technical structure of an argument is called Formal Fallacy.
Informal Fallacies: Informal fallacies are a matter of unclear expression that deal with the logic of the meaning of language. Opposite to it, formal fallacies deal with the logic of the technical structure.
An informal fallacy involves such things as:
- the misuse of language such as words or grammar,
- misstatements of fact or opinion,
- misconceptions due to underlying presuppositions, or
- just plain illogical sequences of thought.
Uses of Language in Logic
A logic always deals with the analysis and evaluation of arguments. Since arguments are expressed in language, the study of arguments requires a carefully attention to language in which arguments are expressed.
The followings are three important uses of language:
- Informative,
- Expressive and
- Directive uses of language.
Informative use of language: It involves an effort to communicate some content or to describe something or to give information about something. When I say a child, “The Second of October is the Gandhi Jayanti.” The language I used is informative.
This kind of use of language presumes that the content of what is being communicated is true, so it will be our main focus in the study of logic.
When a sentence is used informatively, it reports that something has some feature or that something lacks some feature. Consider the following two sentences:
- Parrot has a feather.
- Parrot is not mammals.
The first proposition reports that having feather is a feature of a Parrot. The second proposition reports that Parrot do not have some essential qualities found in mammals. In, both cases it provides information about the world.
Two main aspects of this function are generally noted: (1) evoking certain feelings and (2) expressing feelings.
Expressive discourse, qua expressive discourse, is best regarded as neither true or false.
Expressive use of Language: This type of language is often used to express our emotions, feelings, or attitudes. For example: It’s too bad!, It’s wonderful!, etc.
When language is used expressively or emotively, it cannot be characterized as true or false.
Directive uses of language: When the use of language is often to give direction as Commands, requests, instructions, questions etc., to do or not to do something.
Consider the following examples:
- Finish your homework.
- Wash your clothes.
- Are you feeling well?
In all the above examples, the directive use of language. Directive use of language is not normally considered true or false (although various logics of commands have been developed).
Connotations and denotations of terms
Denotation is the dictionary definition or literal meaning of a word only. Not emotions or feelings are associated with the word.
Ex: The teacher walked into the classroom. This example does not have any hidden meaning. A teacher simply walked into a classroom.
Connotation: A word’s emotional meaning; suggestions and associations that are connected to a word. Words can be positive, negative, or neutral. Words can also connote specific feelings or emotions.
Different types of Definition
Lexical: The purpose of a lexical definition is to report the way a word is standardly used in a language. Most definitions found in a dictionary are lexical definitions.
Ex. Fossil, Cat, Dogs etc.
Persuasive: The purpose of a persuasive definition is to influence people’s attitudes, not to neutrally and objectively capture the standard meaning of a word.
Eg. Teenagers, Abortion etc.
Stipulative: A stipulative definition stipulates (assigns) a meaning to a word by coining a new word or giving an old word a new meaning. A stipulative definition is neither true nor false; it is neither accurate nor inaccurate.
Eg. Sugarnecker, Black Holes, etc.
Theoretical: Theoretical definitions can explain concepts theoretically. Sometimes definitions are given for terms, not because the word itself is unfamiliar, but because the term is not understood. Such concepts require theoretical definitions, which are often scientific or philosophical in nature.
For example, when your chemistry teacher defines water by its chemical formula H2O, he is not trying to increase your vocabulary (you already knew the term water), but to explain its atomic structure.
Accepting a theoretical definition is like accepting a theory about the term being defined. If you define spirit as “the life-giving principle of physical organisms,” you are inviting others to accept the idea that life is some how a spiritual product.
Precising: A precising definition takes a word that is normally vague and gives it a clear precisely defined meaning.
Eg. Lite, Low-income, middle aged, etc.
Related Topics:
UGC NET Syllabus (Updated): Paper 1 and 2
Solved Question Papers of UGC NET Paper 1
UGC NET Study Materials for Paper 1 (Download PDF)
Official Website for UGC NET
Such simple explanation,simply wow.
Thanks for the appreciation.
good explanation !!!
Good work ….
you are doing great work
Thanks for the Appreciation.
Please share among your firends circle through all mode of social media.
Scholarify Team