
Mathematical Aptitude is a way to identify the basic mathematical skill of the candidates. We all aware of the fact that after clearing the UGC NET exam, we will go for either teaching at colleges/universities level or enroll for Ph.D. In both cases, we need basic mathematical skills for calculation, analysis, grading, percentage, etc.
Mathematical Aptitude
In UGC NET Syllabus of Paper 1, the following topics of mathematical Aptitude are mentioned:
UNIT V – Reasoning (including Mathematical) (Click on the topic to read)
|
UGC NET Study Materials for Paper 1 (eBook with MCQs) Download Now |
Online Course for Mathematical Aptitude Paper 1
This online course covers the entire syllabus of Unit – Mathematical Reasoning and Aptitude
with Practice Quizzes and PDF materials

Fraction
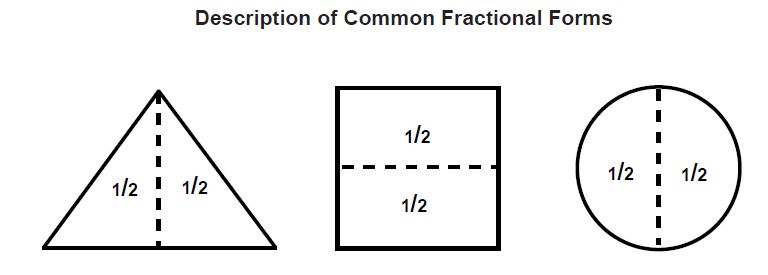
A fraction is a part of a whole unit or quantity. For example, if a square, triangle, or circle is divided into two equal parts, one of these parts is a fraction of the whole square, triangle, or circle.
Points:
- A fraction represents one or more equal parts of a whole.
- The number above the line in a fraction is called the numerator and the number below the line is called denominator of the fraction.
- When the numerator and denominator of a fraction are equal then, the fraction equals 1.
- There are as many ways to write 1 as a fraction as there are numbers.
- Fractions that have the same denominator are said to have a Common Denominator.
Example: 5/10, 5 is the numerator, and 10 is the denominator.
Ratio
- A ratio is a comparison of two quantities
- A ratio is simplified the same way that a fraction is simplified.
- A ratio can be inverted and still be true.
Proportion and Percentage
A proportion is simply a statement that two ratios are equal. It can be written in two ways: as two equal fractions, a/b = c/d; or using a colon, a:b = c:d.
The following proportion is read as “twenty is to twenty-five as four is to five.”
20/25 =4/5
In problems involving proportions, we can use cross products to test whether two ratios are equal and form a proportion. To find the cross products of a proportion, we multiply the outer terms, called the extremes, and the middle terms, called the means.
Percentage
The use of percentages is a commonplace in many aspects of commercial life. Interest rates, discounts, pay rises, and so on are all expressed using percentages.
Any fraction which has a denominator of 100 can be written in a special way known as a percentage. The symbol for percentage is %.
For example, the fraction 20/100 is written as 20%, and this is read as ‘twenty percent’.
Proportion and percentage are very important for calculation in Data Interpretation. The question of Data Interpretation is generally related to percentages like finding growth, increment, loss, etc.
Averages
The average is defined as the sum total of all volumes of items divided by the total number of items.
- Arithmetic average is used for all averages like: average income, average profit, average age, average marks etc
- In individual series. Average = sum of observation / Number of observation
or x ̅=(x^1+x^2+x^3+⋯+x^n)/n - To calculate the sum of observations, they should be in the same unit
Example: Ram, Shyam, David, and Abbas are students, and they have Rs. 200, Rs. 300, Rs. 500, and Rs. 600 respectively. What is the average amount they have?
Ans. Total amount = 200+300+500+600 = Rs. 1600
Total Number of Students = 4
Then, Average money they have = 1600/4 = Rs. 400
Example: A man purchased 5 toys at the rate of Rs 200 each, and 9 toys at the rate of Rs 300 each. Calculate the average cost of one toy.
Solutions: Price of 5 toys = 200 x 5 = 1000
Price of 6 toys = 250 x 6 = 1500
Price of 9 toys = 300 x 9 = 2700
Average cost of one toy = (1000+1500+2700)/20= 5200/20= Rs. 260/-
Time & Distance
Times and distance is a very important topic of Mathematical Aptitude for general competitive exams, like Banking, Railways, SSC etc. But, this is not an important topic in Mathematical Aptitude of UGC NET Exam.
This type of questions ask to test the general mathematical ability.
Points to solve the question
- The speed (rate) at which an object move is a distance that the object covers in a unit of time.
- The formula for the relationship between the speed, the distance the object covers, and the amount of time it requires to cover that distance is:

All possible relationships between distance, speed and time can be derived from this formula:
t = s/v and s = v · t
All possible relationships between distance, speed and time can be derived from this formula:
t = vs and s = v · t
Example: A train traveled 240 kilometers (km) at a speed of 80 kilometers per hour (kph). How long did the journey take?
a) 7 hours b) 5 hours c) 3 hours d) 2 hours
Ans. : c) 3 hours
We are given v (80 kph) and s (240 km), and we have to calculate t. Since the speed is given in kilometers per hour, the traveling time must be calculated in hours.
Substituting the given information into the formula t= s/v ,
we get t = 240/80 = 3
Thus, the journey took 3 hours
Profit & Loss
The calculation of profit and loss involves various terms like cost price, selling price, marked price etc. Basically, it is a difference between cost price and selling price.
- Cost price is the price paid to purchase an article or a product or we can say it is a cost incurred in manufacturing an article.
- Selling price is the price at which a product is sold.
Various profit and loss formulas used in profit and loss:
1. Generally, profit is calculated as: Profit or gain = Selling price(S.P) – Cost price (C.P)
2. Similarly, Loss = Cost price – Selling price
3 Gain percentage (%) = (Gain/ C.P.) ×100
4. Loss percentage(%) = (Loss/ C.P.) ×100
5. There is a direct relationship between selling price and cost price:
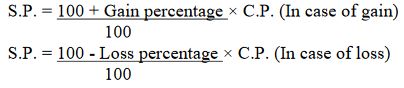
6. If a person sells two commodities at same prices. On one he gains x % and loses x % on another, then as a whole he will be in loss and the loss percentage will be equal to:
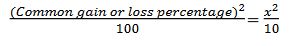
Example: A man buys a cycle for Rs.1400 and sells it at a loss of 15%. What is the selling price of thecycle?
a) Rs.1090 b) Rs.1160 c) Rs.1190 d) Rs1202
Ans. c)
Selling Price = Rs. 1400 – 15 % loss
= Rs. (1400× 85 %) = Rs. 1400 × 85/100
= Rs. 1190
Interest & Discounting
This topic is also based on percentages and simple calculations like profit and loss. The questions related to interest and discounting never asked in previous exams since June 2012.
The mathematical Aptitude is a lengthy topic and needs the prior basic mathematical calculation to attempt the questions.
Note: If you are not interested or uncomfortable in solving the questions related to mathematical Aptitude. We advise you to keep away from this topic, otherwise trying to solve these questions without a regular practice would be spoiled the UGC NET paper 1 during the exam.
Keep practice and practice. If you feel that now you can solve the question easily, then attempt the questions in the exam.
Related Topics:
UGC NET Syllabus (Updated): Paper 1 and 2
Solved Question Papers of UGC NET Paper 1
UGC NET Study Materials for Paper 1 (Download PDF)
Official Website for UGC NET
It’s really helpful